상관계수(Correlation Coefficient)
두 변수 사이의 선형관계를 정량화한 하나의 숫자
일반적으로 피어슨 상관계수를 의미한다.
상관관계를 다룰 때는 인과관계가 아님을 의식하고 있어야 한다.
피어슨 상관계수
두 변수 X와 Y간의 선형 상관관계를 계량화한 수치
코시-슈바르츠 부등식에 의해(?) 범위는 -1부터 1까지이다.
-1은 완벽한 음의 관계,1은 완벽한 양의 관계, 0은 선형관계가 없음을 의미한다.
가정
데이터셋을 생성할 때, np.random.randn 함수를 사용해 요소들을 표준 정규분포된 난수로 구성하길래 왜 그런가 하여 찾아보니 피어슨 상관계수를 사용하기 위한 가정들이 존재했다.
- 두 변수가 정규 분포를 따라야 한다.
- 두 변수가 선형관계에 있어야 한다.
- 두 변수가 독립적이다.
- 두 변수의 분산이 동일해야 한다.
(검색 결과 각 자료마다 이견이 있지만, 공통되고 이론적인 가정들을 가져왔다. 아래 링크를 참고.)
수학적 정의
비례척도의 데이터에서 두 변수의 공분산을 각각의 표준편차의 곱으로 나눈 값
위 가정을 만족하지 않는 데이터에 대해서는 기타 계산(분산과 표준편차를 구하여 다시 계산)을 거쳐야 하겠지만 이 책에서는 딥하게 다루지 않는 듯하다.
이미 np.random.randn 함수를 통해 표준 정규분포를 따르는 요소로 구성했으므로 피어슨 상관계수를 구하기 위해 평균 중심화와 정규화 과정만이 필요한 것 같다.
각 변수의 평균 중심화
평균 중심화란 각 데이터 값에서 평균값을 뺴는 것.
벡터 노름 곱으로 내적을 나누기
정규화를 통해 측정 단위를 제거해 상관계수의 최대 크기를 |1|로 제한
피어슨 상관계수를 파이썬으로 구현
import numpy as np
def get_pearson(x,y):
x_mean=np.mean(x)
y_mean=np.mean(y)
return np.dot(x-x_mean,y-y_mean)/(np.sqrt(np.sum((x-x_mean)**2))*(np.sqrt(np.sum((y-y_mean)**2))))
x=np.random.randn(15)
y=np.random.randn(15)
print(f'직접 구현한 피어슨 계수 함수로 구한 피어슨상관계수:{get_pearson(x,y)}')
print(f'np.corrcoef를 사용해 나타낸 피어슨 상관계수:{np.corrcoef(x,y)[0,1]}') #corrcoef 함수가 correlation coefficient로 이루어진 행렬을 return하므로 [0,1]요소를 출력.np.corrcoef(x,y,rowvar,dtype) 함수에 대하여.
- x,y는 상관계수를 비교할 데이터 셋이다. 각 데이터셋은 $M\times N$ 행렬로 이루어진다.
- rowvar가 True면 행을 하나의 데이터로 간주(데이터가 N개), False면 Column을 하나의 데이터로 간주(데이터가 M개) default로 True다.
- dtype은 data-type을 뜻한다. default로 float형이 설정되어 있다.
쉽게 설명하자면, 행렬 X가 2*2, 행렬 Y가 1*2 이면 X의 1행,2행이 각각 데이터 배열이 된다.
Y는 1행이 데이터 배열이 된다.
| X1 | X2 | Y1 | |
|---|---|---|---|
| X1 | 1 | ||
| X2 | 1 | ||
| Y1 | 1 |
를 비교해서 X1과 X1, X1와 X2, X1과 Y1... 을 비교해 상관계수를 구하고 행렬을 채워 반환한다.
따라서 대각선 성분은 같은 데이터를 비교하는 것이므로 항상 1이 된다.
Cosine Similarity
두 변수간의 유사성을 평가하는 방법으로 코사인 유사도가 존재.
내적의 기하학적 공식으로 코사인 값을 구하는 걸 말함.
$cos(\theta_{x,y})=\frac{x \cdot y}{||x||||y||}$
비슷하지만 피어슨 상관계수와는 다른 공식이다.
피어슨 상관계수는 서로 다른 조건을 가정하기 때문에 값이 같을 수 없다.
피어슨 상관관계와 코사인 유사도의 차이
피어슨 상관관계 관점에서는 [0,1,2,3]이나 [100,101,102,103]은 상관계수 1을 가진다.(완벽한 상관관계)
평균중심화와 정규화를 진행하기 때문에 값의 크기 자체는 상관이 없다.
반면에 코사인 유사도는 0.808이 나오게 되는데 위 과정을 하지 않았기 때문.
코사인 거리
코사인 유사도를 구현한 라이브러리는 찾을 수 없었다. 책에서는 spatial.distance.cosine함수를 사용해보라고 되어있는데 이는 코사인 거리를 구현해놓은 함수다.
코사인 거리란 무엇일까
$코사인 거리 =1- 코사인 유사도$
위와 같은 식으로 코사인 거리는 정의된다. 유사할수록 거리는 가까워진다(즉, 유사도가 1에 근접할수록 거리는 작아진다.)는 개념에 의한 공식이라고 볼 수 있다.
코사인 유사도는 각에 의한 유사도를 따진다고 볼 수 있다.
코사인 거리는 길이에 의한 유사도를 의미한다고 볼 수 있을까?
코사인 거리는 거리 함수일까?
답은 그렇지 않다.이다.
아래 출처의 자료에서는
- 삼각부등식을 만족하지 않는다.
- 수치적으로 부정확하다.
- 삼각함수 계산 자체가 느리다.
그렇다고 안쓰는 것이 아니라 유사도를 계산하는 지표로서 의미가 있고
코사인 유사도는 각도 측면에서 봤을 때도 의미가 있기 때문에 상황에 맞게 적절한 방법을 택하면 된다고 한다.
코사인 유사도를 파이썬으로 구현
import numpy as np
from scipy import spatial
def get_CosineSimilarity(x,y): #직접 구현한 코사인 유사도 함수
return np.dot(x,y)/(np.linalg.norm(x)*np.linalg.norm(y))
x=np.random.randn(15)
y=np.random.randn(15)
print(f'직접 구현한 코사인 계수 함수로 구한 코사인 계수:{get_CosineSimilarity(x,y)}')
print(f'spatial.distance.cosine를 이용해 나타낸 코사인계수:{1-spatial.distance.cosine(x,y)}')연습문제 풀이
[0,1,2,3]과 이 배열에 특정 offset을 더한 두 번째 데이터 배열이 존재할 때, 둘의 피어슨 상관계수와 코사인 유사도를 계산하는 문제를 풀어보았다.
여기서 offset은 -50에서 50까지 1씩 변하는 변수다.
코드
import numpy as np
import matplotlib.pyplot as plt
from scipy import spatial
x=np.array([0,1,2,3])
offset_list=np.arange(-50,51)
r=np.zeros((len(offset_list),1))
c=np.zeros((len(offset_list),1))
for i in range(len(offset_list)):
y=x+offset_list[i]
r[i]=np.corrcoef(x,y)[0,1]
c[i]=1-(spatial.distance.cosine(x,y))
plt.figure(figsize=(10,10))
# make the plot look a bit nicer
plt.scatter(offset_list,r,label='Pearson')
plt.scatter(offset_list,c,label='Cosine-Similarity')
# plt.axis('square')
plt.axis([-50,50,-1,1.3])
plt.xlabel('average offset')
plt.ylabel('r or c')
plt.legend()
plt.title('figure 3-4')
print(c)
plt.show()결과
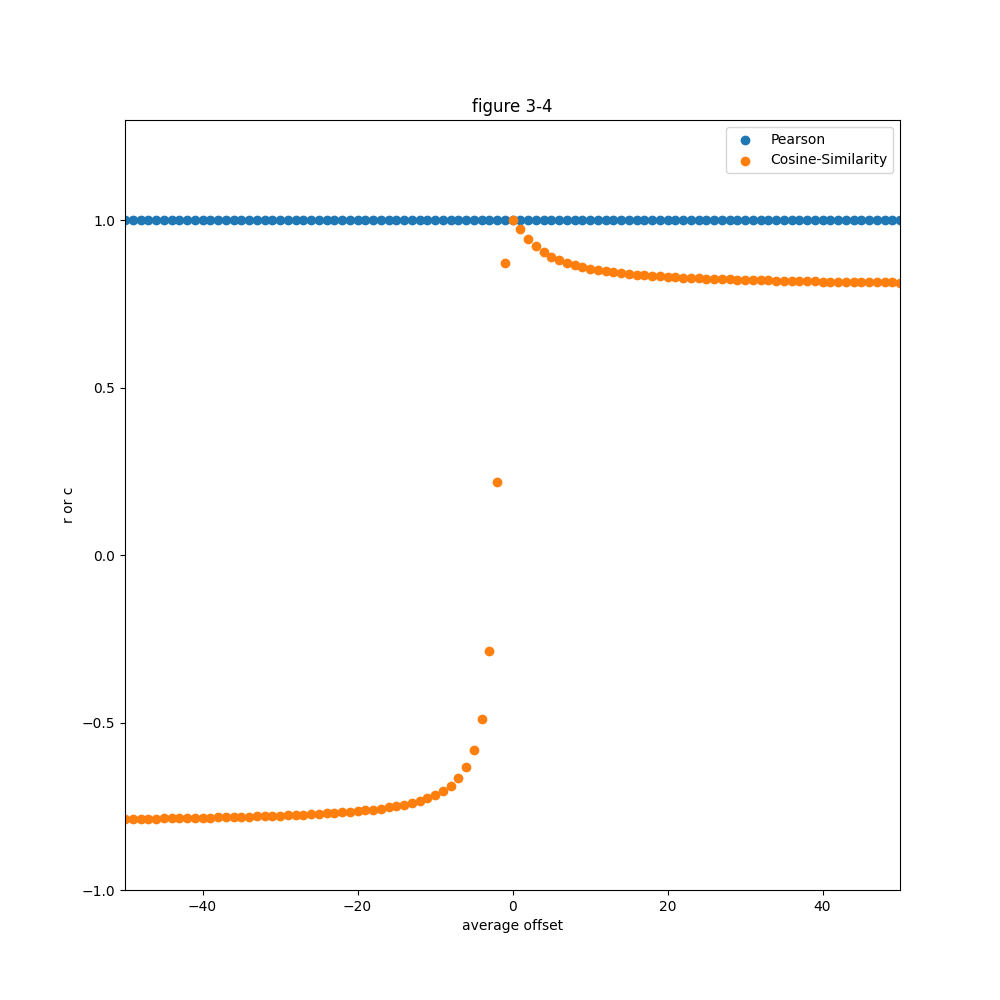
결론
- 피어슨 상관계수는 항상 1이다.
왜냐하면 평균중심화를 진행해보면 당연히 같을 수 밖에 없다. offset이 얼마든 간에 평균중심화를 거치면 [0,1,2,3]과 같다. 여기에 정규화를 진행하면 상관계수가 같을 수 밖에 없는 것이다. - 코사인 유사도는 0을 기준으로 음에서 양으로 바뀐다.
코사인 유사도는 기본적으로 두 데이터가 이루는 각을 바탕으로 유사도를 계산하는 방법이다.
오프셋이 음수면 두 데이터의 내적값이 음수가 되고, 양수면 내적값도 양수가 되는 것이 기본적으로 부호가 바뀌는 이유다.
오프셋이 0일 때, 두 데이터가 같아지므로 1이 되고 $|offset|$이 커질수록 $|Cosine Similarity|$가 커진다. 허나, 하나의 데이터가 [0,1,2,3]으로 고정되어 있고 값 자체가 작기 때문에 0.75정도로 값을 이루는 것으로 추측된다.
출처
'Linear Algebra > 개발자를 위한 실전 선형대수학' 카테고리의 다른 글
| [파이썬과 선형대수] 행렬 곱셈을 통한 기하학적 변환 (1) | 2024.10.31 |
|---|---|
| [파이썬과 선형대수] 다변량 공분산 행렬에 대해 알아보자! (2) | 2024.10.29 |
| [파이썬과 선형대수] 'k-mean clustering'에 대해 알아보자! (0) | 2024.10.23 |
| [파이썬과 선형대수]Low-Pass Filter/High-Pass Filter를 구현해보자! (1) | 2024.10.21 |
| [파이썬과 선형대수] 시계열 필터링과 특징 탐지 (0) | 2024.10.18 |

