필터링, 시계열 필터링에 대해서 알아보자.
필터링
먼저 필터링에 대해서 알아야 한다. 필터링이란, 뭔가를 걸러낸다는 뜻으로 많이 사용된다.
신호 및 시스템과 같은 과목에서의 필터링은 불필요한 노이즈를 걸러내고 필요한 데이터를 추출한다는 뜻으로 사용된다.
어떤 신호에서 특징을 감지하는 기법을 필터링이라고 한다. Kernel(즉, 필터 역할)와 신호의 일부의 연산을 통해 일치하는 특징을 찾아낸다.
시계열 필터링
이론적으로는 Continuous-Time(연속적인 시간)에 대하여 계산을 한다.
하지만 현실 세계의 신호들은 아날로그 신호이기 때문에 Discrete-Time(불연속적인 시간)에 대해서 필터링하는 게 대부분이다.
필터링을 할 때, 지역 특징 탐지를 해야 하고 커널의 길이는 유한하다. 따라서 신호를 커널의 길이에 맞게 슬라이스 하여 내적을 계산한다. 해당 시점에서의 내적값은 해당 시점에서의 필터링 값이 되고 구간을 이동시키면서 계산을 반복한다.
위 과정을 합성곱(convolution)이라고 한다.
대표적인 시계열 필터링으로 에지(edge) 검출 필터, 저주파(low-pass) 필터, 고주파(high-pass) 필터 등이 있다.
필터링할 때, 왜 내적(Inner Product)을 사용할까?
왜 내적을 사용하는지 알기 위해서는, 내적의 의미에 대해 생각해봐야 한다.
내적은 두 벡터 간의 연산으로, 두 벡터 a,b 가 주어졌을 때, $|a||b|cos(\theta)$ 로 계산된다.
두 벡터가 이루는 각도가 작아질수록 내적값은 커지고 두 벡터가 유사하다고 할 수 있다.
필터링의 목적이 커널과 유사한 데이터를 찾아내는 것이기 때문에 내적을 사용한다고 생각해 볼 수 있다.
에지 검출기 구현
에지 검출기의 목적은 아날로그 신호가 0에서 1로 혹은 반대로 바뀌는 시점을 찾아내는 것이다.

kernel은 [-1 1]이고 clock signal은 0이다가 t=10에서 1로 바뀌고 t=20에서 0으로 떨어지는 꼴이다.
에지 검출기는 t=10과 t=20에서 에지가 생겼음을 찾아내야 한다.
계산과정
kernel이 [-1 1]이라 했다. signal의 t=0일 때 [0 0]으로 슬라이스할 수 있다. 둘의 내적값은 0이다.
t=1일 때도 [0 0]이므로 내적값이 0이다.
t=10일 때 [0 1]이므로 내적값이 1이고 t=20일 때 내적값이 -1이다.
따라서 필터링한 결과는 t=10일 때 1, t=20일 때 -1, 이외의 구간은 0으로 나타나야 한다.
아래는 파이썬으로 구현한 에지 검출기
import matplotlib.pyplot as plt
import numpy as np
plt.figure(figsize=(10,10))
#그림A(kernel)
plt.subplot(2,2,1)
kernel=np.array([-1,1]) #kernel 배열 생성
x=np.array([15,16])
plt.axis([-1,30,-1.25,1.25]) #축 설정
plt.plot(x,kernel,'ks-',)
plt.title('kernel')
#그림B(clock signal)
plt.subplot(2,2,2)
x2=np.arange(30) #x 데이터 생성
y2=np.zeros(30) #y 데이터가 될 배열 생성
y2[10:20]=1 #슬라이싱을 통해 신호 배열을 만들어줌.
plt.axis([-1,30,-0.25,1.25])
plt.plot(x2,y2,'ks-')
plt.title('Clock Signal')
#그림C(after filtering)
plt.subplot(2,2,3)
length=len(x2)
y3=np.zeros(length) #필터링 결과가 들어갈 배열 생성
for i in range(1,length-1): #구간 이동을 위한 for 반복문
y3[i]=np.dot(kernel,y2[i-1:i+1]) #주어진 구간의 신호와 kernel을 내적
plt.axis([-1,30,-1.25,3.5])
plt.plot(x2,y3,'bs-')
plt.plot(x2,y2,'ks-')
plt.title('Result')
plt.show()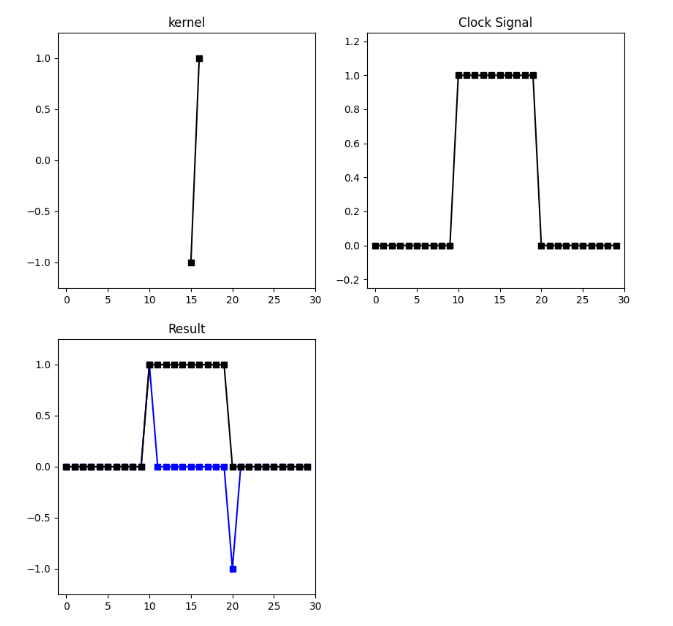
파란색이 필터링된 결과다. 정확히 에지 부분에서 1과 -1로 그래프가 튀고 이외의 시점에서는 모두 0이다.
반대로 kernel을 [1 -1]로 해보면 어떨까.
튄 그래프 부분이 반대로 뒤집히지 않을까

kernel을 비대칭적으로 [-1 2] 와 같이 해본다면 어떻게 될까.

우연히 엣지부분을 검출하면서도 신호를 그대로 따라가게끔 나타났다.
kernel에 따라 필터링 결과가 달라지니 kernel을 무엇으로 할지 정하는 것이 중요한 포인트이겠다.
이어서 Low-pass Filtering과 High-pass Filtering 도 알아볼 예정이다.
'Linear Algebra > 개발자를 위한 실전 선형대수학' 카테고리의 다른 글
| [파이썬과 선형대수] 행렬 곱셈을 통한 기하학적 변환 (0) | 2024.10.31 |
|---|---|
| [파이썬과 선형대수] 다변량 공분산 행렬에 대해 알아보자! (1) | 2024.10.29 |
| [파이썬과 선형대수] 'k-mean clustering'에 대해 알아보자! (0) | 2024.10.23 |
| [파이썬과 선형대수]Low-Pass Filter/High-Pass Filter를 구현해보자! (1) | 2024.10.21 |
| [파이썬과 선형대수] 상관관계와 코사인 유사도에 대해 알아보자! (0) | 2024.10.19 |