행렬의 기하학적 관점
행렬을 기존과 다르게 기하학적 관점으로 살펴볼 수 있다.
흔히 변환 행렬(Transformation Matrix) 라고 부르는데 종류는 여러 가지가 있다.
스케일 행렬,회전행렬 등 여러 가지의 종류가 존재한다.
오늘은 스케일 행렬과 회전 행렬에 대해 알아보자.
스케일 행렬(Scale Matrix)
스케일 행렬은 기본적으로 벡터의 크기를 조절하는 역할이다.
행렬의 대각 성분이 스케일의 역할을 담당하기 때문에 기본적인 스케일 행렬은 대각행렬이다.
계산은 아래 그림처럼 되고 각 성분의 크기를 조절할 수 있다.
회전 변환 행렬(Rotation Matrix)
가장 기초적인 변환 행렬은 회전 변환 행렬이다.
$\begin{pmatrix}cos(\theta)&sin(\theta)\\-sin(\theta)&cos(\theta)\end{pmatrix}$
위 행렬은 길이를 유지하면서 벡터를 회전시키는 '순수 회전 행렬'이다.
$\theta=0$이면 회전을 하지 않는다.
회전 변환 행렬도 $I$가 되어 회전시키지 않는 것과 같다.
말만으로 하면 이해가 잘 안 되니 직접 계산을 해보자.
(2,0)을 90도 회전해서 (0,2)가 됨을 알 수 있다.
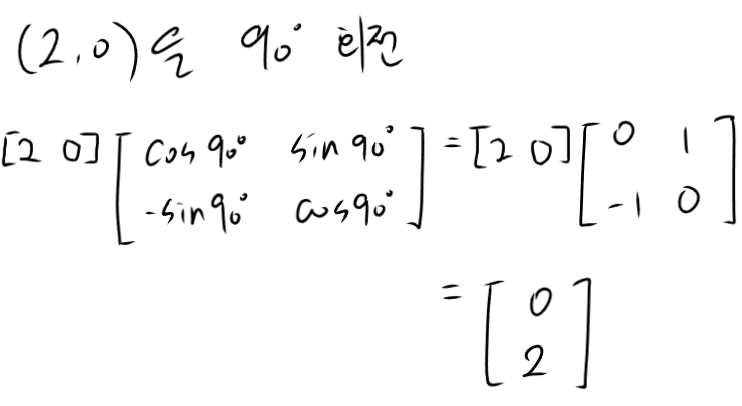
타원을 회전
도형을 회전할 때에도 회전 행렬이 사용된다. 그 예시로 타원을 회전하는 코드를 짜보았다.
아래는 $\frac{x^2}{9}+\frac{y^2}{4}=1$ 타원이 45도 회전하게 하는 코드이다.
사용한 회전 행렬은 아래와 같다.
$\begin{pmatrix}cos(\frac{\pi}{4})&sin(\frac{\pi}{4})\\-sin(\frac{\pi}{4})&cos(\frac{\pi}{4})\end{pmatrix}$
코드
import numpy as np
import matplotlib.pyplot as plt
theta=np.linspace(0,2*np.pi,50) #세타의 범위 0부터 2pi까지
points=np.vstack([3*np.cos(theta),2*np.sin(theta)]) #타원을 극좌표로 표현했다.
T=np.array([[np.cos(np.pi/4),np.sin(np.sin(np.pi/4))]
,[-np.sin(np.pi/4),np.cos(np.pi/4)]]) #45도 회전 행렬
new_points=T@points #행렬을 곱한다.
rotate_opposite=points.T@T #반대로 곱한다.
# ploting eclipse
plt.plot(points[0],points[1],'ks-')
plt.plot(new_points[0],new_points[1],'bs-')
plt.plot(rotate_opposite.T[0],rotate_opposite.T[1],'rs-')
plt.axhline(y=0,color='k',linewidth=1)
plt.axvline(x=0,color='k',linewidth=1)
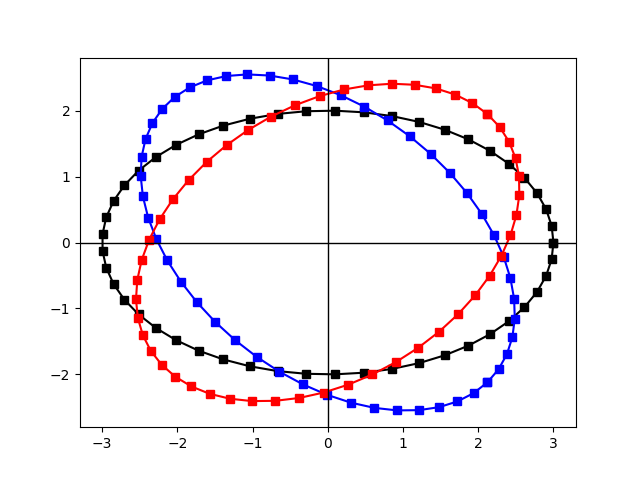
plt.show()실행결과
결론
먼저 T@points으로 계산한 타원이 파란색 타원이다. 시계 방향으로 45도 돌아갔다.points.T@T는 빨간색 타원이다. 반시계 방향으로 45도 돌아갔다.
앞에서 곱하느냐 뒤에서 곱하느냐도 회전 방향에 영향을 준다.
추가 응용
여기에 스케일 행렬을 추가해 보자.
기존 행렬 T의 대각 성분에 2를 곱해보았다.
$\begin{pmatrix}2\times cos(\frac{\pi}{4})&sin(\frac{\pi}{4})\\-sin(\frac{\pi}{4})&2\times cos(\frac{\pi}{4})\end{pmatrix}$
실행 결과는 아래와 같다.
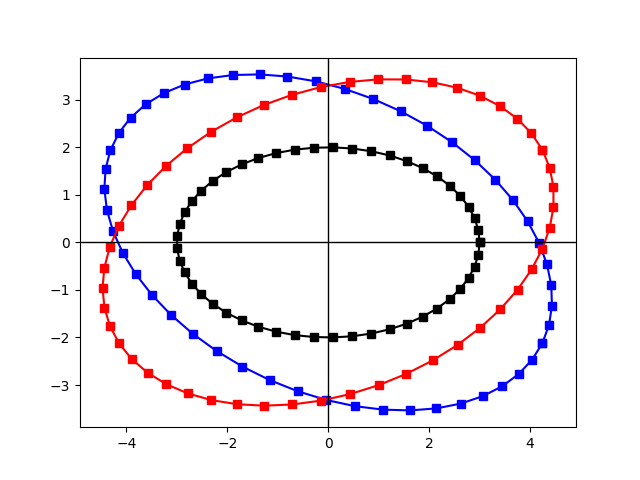
대각 성분에 2씩 곱해졌다는 것은 타원이 2배 커졌다는 뜻이다.
$\begin{pmatrix}2\times cos(\frac{\pi}{4})&sin(\frac{\pi}{4})\\-sin(\frac{\pi}{4})&2\times cos(\frac{\pi}{4})\end{pmatrix}=\begin{pmatrix}2&0\\0&2\end{pmatrix}\begin{pmatrix} cos(\frac{\pi}{4})&sin(\frac{\pi}{4})\\-sin(\frac{\pi}{4})&cos(\frac{\pi}{4})\end{pmatrix}$
이기 때문에 45도 회전하면서 2배 커진 타원이 나타나는 것이다.
출처
서적
개발자를 위한 실전 선형대수학/한빛미디어/마이크, 코헨 지음
WebSite
'Linear Algebra > 개발자를 위한 실전 선형대수학' 카테고리의 다른 글
| [파이썬과 선형대수] 역행렬(1) (정의, 조건, 구하는 법, 유일성) (0) | 2024.11.10 |
|---|---|
| [파이썬과 선형대수] 이미지 필터링에 대해 알아보자! (0) | 2024.11.03 |
| [파이썬과 선형대수] 다변량 공분산 행렬에 대해 알아보자! (1) | 2024.10.29 |
| [파이썬과 선형대수] 'k-mean clustering'에 대해 알아보자! (0) | 2024.10.23 |
| [파이썬과 선형대수]Low-Pass Filter/High-Pass Filter를 구현해보자! (1) | 2024.10.21 |
